How do you measure the value of reduced mortality from a specific disease? Just because you are less likely to die from AIDS in a given year does not mean that your likelihood of dying from cancer will decrease. Thus, how does one model the monetary value of a decrease in disease-specific mortality within a competing risk model. Today, I review a paper by Becker, Philipson and Soares who describe one approach for measuring this quantity in practice.
Theory
Consider the following utility maximization problem using the indirect utility function V(Y,S) where Y is lifetime income and S is the survival function.
- V(Y, S) = max ∫exp(ρt)S(t)u(c(t))dt
subject to
- Y = ∫ exp(−rt)S(t)y(t)dt = ∫exp(−rt)S(t)c(t)dt
where y(t) is income at age t, c(t) consumption at t, and r is the interest rate.
The goal of this analyis is to find how much additional survival is worth; in other words, how much less money would a person be willing to accept to live a longer life. Mathematically this means finding E where:
- V(E + Yτ+∆τ,Sτ) = >V(E + Yτ+∆τ,Sτ+∆τ)
To simplify the analysis, assume that individual’s discount rate, ρ, is equal to the interest rate, r, across all time periods and that r is constant over time. In this case, the optimal consumption path is to consume the same amount every period. Thus, c(t) = c = y where c and y are year consumption and income respectively. Thus, one can rewrite the indirect utility function as:
- V(Y, S) = u(y)∫exp(-rt)S(t)dt
.
Further simplify the analysis by defining A(S) as as the value of an annuity based on the survival function S as follows:
- A(S) = ∫exp(-rt)S(t)dt
If e is the yearly income that compensates for lower longevity, then e must satisfy the following condition:
- u(e+yτ+∆τ)A(Sτ) = u(yτ+∆τ)A(Sτ+∆τ)
One can use a first order Taylor expansion of u() around yτ+∆τ to approximate u(e + yτ+∆τ) as u(yτ+∆τ) + u'(yτ+∆τ)e and substitute into the expression above to get:
- e = (u/u’)*[(A(Sτ+∆τ-A(Sτ+)/A(Sτ+∆τ]
or equivalently
- e/yτ+∆τ = 1/[ε(yτ+∆τ)]*[(A(Sτ+∆τ-A(Sτ+)/A(Sτ+∆τ]
where ε(.) is the elasticity of the utility function and the term in brackets on the right hand side is the percentage increase in annuity that would occur due to the change in the survival function.
Interpretation of Theory
The authors summarize the implications of the equation outlined above as follows:
[The] two dimensions summarized in this expression will be very important in our analysis: the level of income (or consumption) throughout life (term outside brackets), and the size and moment of the reductions in mortality (term inside brackets). Whenever income and longevity are positively correlated across countries, the willingness to pay for an increase in life expectancy will 11 generally have two offsetting components. Richer countries attach more value to given longevity gains (higher u/u’), and countries with higher longevity attach less value to given absolute longevity gains (higher A(Sτ). The effect of income comes from the fact that marginal extensions in life expectancy are more valuable the higher is consumption in this extended lifetime, or, in other words, the higher is the income level.
Empirical Estimation
Survival in a given year implies surviving all disease. This means not only must you must not die from cancer in a given year to survive, you also must not die from AIDS, from Hepatitis, from pneumonia, etc. Thus, one can construct an all cause survival function as:
- S=S1S2S3…SK = Π(k=1 to K) Sk
Define the value (in annual income) of the longevity gain associated with the kth cause of death as the ek implicitly determined by the following expression:
- u(ek + yτ+∆τ)A(Sτ) = (yτ+∆τ)A(S*kτ+∆τ)
where
- S*kτ+∆τ = Skτ+∆τ * ΠΠ{(i≠K)Siτ
S*kτ+∆τ counterfactual survival function, simulating the survival function that would exist in period τ +∆τ, had the mortality rates for all causes of death but k remained at their τ period levels.
The marginal effect of improved overall survival from a change in survival in one component is:
- (∂S/∂τ) = Σ(i=1 to K) [Π{(i≠K) Sk}(∂Si/∂τ)]
The inframarginal effect of a change is the following:
- S*kτ+∆τ – Sτ = [Π{(i≠K)Siτ](Skτ+∆τ – Skτ)
as long as one assumes that the complementary nature of mortality rates is not small in magnitude (e.g., reducing mortality from cancer may increase or decrease mortality from all other sources.
Value of Life
The authors then apply a number of assumptions regarding the fucntional form of the utility function. Specifically, they assume that the utility function takes the following form:
- u(c) = [(c(1-1/γ))/(1-1/γ)] + α
where α is the parameter that arises from the normalization of utility in the death state to zero and γ is the inter-temporal elasticity of substitution.
Using this functional form, the monetary value of a change in life expectancy is:
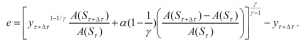
Source:
- Gary S. Becker, Tomas J. Philipson, Rodrigo R. Soares. THE QUANTITY AND QUALITY OF LIFE AND THE EVOLUTION OF WORLD INEQUALITY, NBER Working Paper #9765, June 2003.
- Gary S. Becker, Tomas J. Philipson and Rodrigo R. Soares. The Quantity and Quality of Life and the Evolution of World Inequality. The American Economic Review , Vol. 95, No. 1 (Mar., 2005), pp. 277-291.
1 Comment