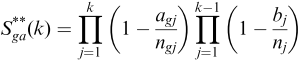This question is not so easy to answer, even when using data from a randomized trial. Further, many studies do not have the statistical power to identify cause-specific mortality. Consider the following example from Kim and Thompson:
Consider a trial of an intervention only influencing a single cause of death, or a few specific causes of death, with corresponding mortality of 5% in the intervention group and 10% in the control group. With other causes of death contributing 30% mortality for the remainder in both groups, total mortality is anticipated to be 33.5% (5% + 30%*95%) in the intervention group and 37% (10% + 30%*90%) in the control group [where the 30% baseline mortality is applied to the number of people who did not die of the specific cause (i.e., 90% and 95%)]. For a sample size of 500 in each group and a type I error of 0.05, this trial would have 82% power to detect the difference in cause-specific mortality, but only 19% power to detect the difference in total mortality.
How does one calculate cause-specific mortality? Cause specific mortality is equal to:
where g is the group (i.e., treatment or control), agj are the number of people who died from group g in year j from the cause of interest, bgj is the number of people who died from other causes, and ngj are the number of people ‘at risk’ of death in group g in year j.
The term  is equal to the Kaplan-Meier survival for total mortality up to period k-1. Typically, agjbgj/(ngj)2 is small, so the last term above approximates the Kaplan Meier survival from the previous period.
is equal to the Kaplan-Meier survival for total mortality up to period k-1. Typically, agjbgj/(ngj)2 is small, so the last term above approximates the Kaplan Meier survival from the previous period.
In practice, Kim and Thompson recommend pooling background survival rates across all groups if any difference in competing risks between two randomised groups is only due to chance. The authors claims that separate background survival functions “…would overestimate life-years gained if the difference in other-cause mortality favoured the same group as the specific cause of interest, and underestimate it if the difference favoured the other group.” Instead, one should estimate the following cause-specific mortality rate as follows:
To estimate these cause-specific survival rates empirically, one can use Lois Kim’s cause-specific cost-effectiveness analysis Stata code available at the MRC Biostatistics Unit.
Source:
- Kim, L. G. and Thompson, S. G. (2011). Estimation of life-years gained and cost effectiveness based on cause-specific mortality. Health Econ., 20: 842–852. doi: 10.1002/hec.1648