Is treatment A better than treatment B? This questions is often difficult to answer, especially if there is not head-to-head evidence comparing the two treatments. In other cases, however, one can use indirect evidence. For instance, one randomized controlled trial (RCT) may compare treatment A to C (e.g., a placebo) and another trial can compare treatment B to C. In this case, one can use meta-analysis to measure the relative effect of A and B by using the C as a control for any trial-specific effects.
Conducting one of these studies, however, is fraught with challenges. To address some of these challenges, an ISPOR Good Practice Task Force developed the following guidelines for indirect treatment comparison/network meta-analysis.
- Did the researchers attempt to identify and include all relevant RCTs? The researchers search use a search strategy that includes all interventions of interest, that uses multiple databases (e.g., MEDLINE, EMBASE, and Cochrane Central Registry of Trials) and selection criteria should admit all RCTs of interest.
- Do the trials for the interventions of interest form one connected network of RCTs? See the discusion below regarding how to estimate treatment effects with a connected network.
- Is it apparent that poor quality studies were included, thereby leading to bias? To address this concern, researchers should provide summary information on key study characteristics of each RCT, such as method of randomization, treatment allocation concealment, blinding of the outcome assessor, and dropout. One option to capture study bias is to use Cochrane Collaboration’s tool for assessing risk of bias in randomized trials.
- Is it likely that bias was induced by selective reporting of outcomes in the studies? Researchers should check to determine whether any of the selected studies do not report some of the outcomes of interest and were therefore not included in some of the network meta-analyses of the different end points. Meta-analyses should clearly state why each study was excluded from the systematic review.
- Are there systematic differences in treatment effect modifiers (i.e., baseline patient or study characteristics that have an impact on the treatment effects) across the different treatment comparisons in the network? An effect modifier alters the measured treatment effect of a study. For example, if a medical intervention works only for men and not for women, a trial among men will demonstrate a positive treatment effect relative to placebo, whereas a trial only among women would not. Sex is a treatment effect modifier for that intervention. If effect modifiers are likely to be present, researchers should compare study-specific inclusion and exclusion criteria, baseline patient characteristics, and study characteristics that are expected to be effect modifiers.
- If yes (i.e., there are such systematic differences in treatment effect modifiers), were these imbalances in effect modifiers across the different treatment comparisons identified before comparing individual study results? Reseachers should generate a list of potential effect modifiers and determine whether there are differences in the effect modifiers either within or between studies. Use of meta-regression or match-adjusted indirect comparison methods are other options to address cases where effect modifiers vary across studies.
- Were statistical methods used that preserve within-study randomization? Typically, this would involve using the Bucher method. (No naive comparisons)
- If both direct and indirect comparisons are available for pairwise contrasts (i.e., closed loops), was agreement in treatment effects (i.e., consistency) evaluated or discussed? Were both direct and indirect estimates presented? In an ABC network that consists of AB trials, AC trials, and BC trials, direct evidence for the BC contrast is provided by the BC trials and indirect evidence for the BC contrast is provided by the indirect comparison of AC and AB trials. Research should compare and contrast the findings from using both direct and indirect evidence.
- Was a valid rationale provided for the use of random-effects or fixed-effect models? A random-effects model assumes that each study has its own true treatment effect, because study characteristics and the distribution of patient-related effect modifiers differ across studies. The study-specific true effects are then assumed to follow a distribution around an overall mean (the meta-analysis mean), and with a variance (between-study heterogeneity) that reflects how different the true treatment effects are between them. In contrast, a fixed-effect (equal-effect) model assumes that the true treatment effect is common in all studies comparing the same treatments. This implies that there are no effect modifiers, or that they have the same distribution across all studies in the meta-analysis. Generally, random effects models should be used unless the fixed effects rational can be justified. Researchers should also discuss what types of heterogeneity exist across trials if the random effects model is used.
- Are the results reported in a transparent, high-quality manner? This includes a graphical representation of the evidence network, reporting individual study results, separating the results of direct and indirect comparisons, and reporting estimates with a 95% confidence interval. If multiple outcomes are measures, treatments should be ranked separately for each outcome. The ranking should take into account the probability one treatment is better than another, not just the measured point estimate. Further, all conclusions should be fair and balanced.
- Are there conflicts of interest? If so, the authors should mentioned them and steps should be taken to mitigate these conflicts of interest.
Estimating treatment effects with a connected network
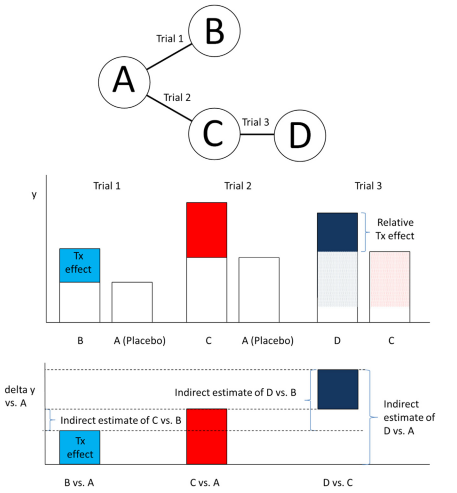
With an indirect comparison, interest centers on the comparison of the treatment effects of interventions that are not studied in a head-to-head fashion. To ensure that the indirect comparisons of interventions are not affected by differences in study effects between studies, we want to only consider the treatment effects of each trial. This consideration implies that all interventions indirectly compared have to be part of one network of trials in which each trial has at least one intervention (such as placebo) in common with another trial.
The figure below demonstrates how the network of RCTs creates estimates of the relative treatment effects across treatments A, B, C and D from data taken from Trials 1, 2 and 3.
The results of a network meta-analysis can be diplayed with a rankogram, which shows the probability that each treatment is best. “For each outcome of interest, the probability that each treat-
ment ranks first, second, third, and so on out of all interventions compared can be called rank probabilities and are based on the location, spread, and overlap of the posterior distributions of the relative treatment effects.”
- Jansen J, Trikalinos TA, Cappelleri JP, et al, Indirect treatment comparison/network meta-analysis study questionnaire to assess study relevance and credibility to inform health care decision-making: an ISPOR-AMCP-NPC Good Practice Task Force report. Value Health 2014;17:157–173.