In general, health economists would like to have health insurers cover treatments that are welfare improving in the Pareto sense. This means, if a treatment provides more expected benefits than costs and no one is worse off (in expectation), then this treatment should certainly be covered. It could be the case, however, that people care who gains the benefits. For instance, consider the case of a new technology that helped people with serious diseases move around more easily inside a mansion. Assume this technology had more benefits than cost. Some (many) people, however, may not like covering a treatment that only benefits people who are very well-off. This issue is especially relevant in single payer systems—like the United Kingdom’s National Health Service (NHS)—which are funded by taxpayers.
One option is to consider both the average net health benefits (i.e., benefits less cost) to a population as well as it’s affect on inequality. If a society doesn’t care at all about inequality, then this reduced to just measuring net health benefit overall; if a society has a strong preference for equality, treatments that provide benefits to only the better off will be considered less valuable.
A paper by Love-Koh et al. 2019 provides a nice quantitative way to estimate these tradeoffs. The approach uses both the Atkinson inequality index and the Kolm index. In the Atkinson index, N is the number of people, Qi is the gain in quality adjusted life expectancy (QALE) for person i, Q_bar is the average QALY for the whole population, and ε is the inequality aversion parameter. The Kolm index is measured similarly. Whereas the Atkinson index measures relative inequality, the Kolm index measures inequality on an absolute scale; also the inequality aversion for the Kolm index is α rather than ε.
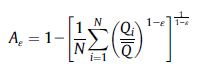
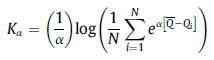
One can use these indices to calculate the equally distributed equivalent (EDE), which is the level of population health (in QALYs) in a completely equal distribution that yields the same amount of social welfare as the distribution under investigation.
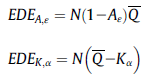
Using this approach, the authors find the following:
Twenty-seven interventions were evaluated. Fourteen interventions were estimated to increase population health and reduce health inequality, 8 to reduce population health and increase health inequality, and 5 to increase health and increase health inequality. Among the latter 5, social welfare analysis, using inequality aversion parameters reflecting high concern for inequality, indicated that the health gain outweighs the negative health inequality impact.
Despite the attractive features of this approach analytically, there are issues related to how it would be implemented. In this case, inequality is based solely on quality-adjusted life expectancy. However, others could take a more holistic approach and look at socioeconomic status including other factors (e.g., income, employment, etc.). In theory, one could perform the same exercise measuring individual overall utility including these other aspects, but few (rightly) would want the government to assess how well people are overall. Second, the authors qualify expected life expectancy by patients’ sex, primary diagnosis and postcode. Thus, you could have a system that prioritizes treatments for men—since men’s life expectancy is generally less than women. Third, this model assumes diseases is exogenous. In many cases this is true, but the in some cases individual behavior could increase the likelihood of having a disease. For instance, would people want to discount treatments for diseaess that are preventable (e.g., lung cancer due to smoking, diabetes due to poor eating habits/exercise). Typically, there are no diseases that are fully exogenous or fully at fault of the individual, so this is a slippery slope.
What the Love-Koh paper contributes is a easy to implement method for quantifying how inequality preferences should affect the value of different treatments. What the paper does not answer is whether this approach should be implemented.
Source:
- Love-Koh J, Cookson R, Gutacker N, Patton T, Griffin S. Aggregate Distributional Cost-Effectiveness Analysis of Health Technologies. Value in Health. 2019 May 1;22(5):518-26.
“its” is misspelled in title.
Good catch. Fixed.