Let’s say you want to measure the causal impact of a specific treatment on patient outcomes from real-world data. Many statistical approaches discuss the appropriate way to estimate this causal effect assuming you know the true data generating function. In practice, however, which variables to include in any regression model may be unclear.
One approach to solve this issue is to use double robust estimators, also known as augmented inverse propensity weighted (AIPW) estimator. Glynn and Quinn (2009) explain why AIPW are so attractive:
AIPW estimator has very attractive theoretical properties and only requires practitioners to do two things they are already comfortable with: (1) specify a binary regression model for the propensity score and (2) specify a regression model for the outcome variable. Most interestingly, the AIPW estimator is doubly robust in that it will be consistent for…[measuring the average treatment effect]…whenever (1) the propensity score model is correctly specified or (2) the outcome regression is correctly specified.
Technically, a double robust estimation has two parts, an inverse probability of treatment weighting (IPTW) section and an “augmentation” section. In the equation below as explained by Jason Roy of the University of Pennsylvania, Y is the outcome, A is whether the individual received the treatment, π(X) is the probability an individual gets the treatment based on their characteristics, and m1(X) is the expected value of Y assuming the patient would have received the treatment conditional on covariates X. The i indexes for individuals. Let’s say that one estimates π(X) with a logit regression and this propensity score does a very good job of estimating whether or not the patient will receive the treatment of interest. In that case, A-π(X) will go to 0 in expectation and AIPW will simplify to the IPTW estimator.
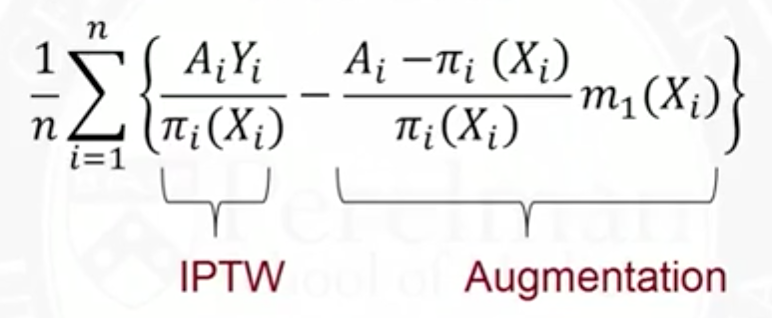
What happens if the propensity score is misspecified. With an AIPW, you still may be in luck. The equation below simply rearranges terms from above. In this case, let’s say that the propensity score is inaccurate but our regression model does a good job of prediction outcomes for people who receive the treatment (i.e., E[Y-m1(X)]=0). Then in this case, the numerator goes to 0 and we are left with a simple regression model.
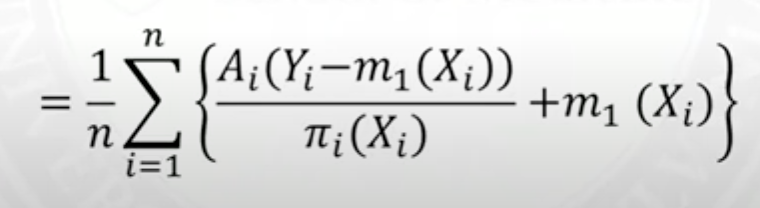
To estimate the outcomes for patients who do not receive the treatment, an analogous approach can be used.
A more detailed, but intuitive description is given in the video below. More formal treatments of AIPW can be found here and here.
How does one estimate AIPW in practice? The following video provides and example using Stata.
And here is an example in R.