When you want to measure the causal impact of an intervention, there are a number of different approaches. Difference in difference (DiD) and the synthetic control method (SCM) are two common methods, each of which I have already provided econometric overview summaries (DiD, SCM). A paper by Arkhangelsky et al (2021) in AER summarizes the difference
In general, DID methods are applied in cases where we have a substantial number of units that are exposed to the policy, and researchers are willing to make a “parallel trends” assumption that implies that we can adequately control for selection effects by accounting for additive unit- specific and time- specific fixed effects. In contrast, SC methods, introduced in a setting with only a single (or small number) of units exposed, seek to compensate for the lack of parallel trends by reweighting units to match their pre- exposure trends.
Arkhangelsky and co-authors also argue that the answer shouldn’t be whether to use DiD or SCM; but rather we should use DiD and SCM via their proposed synthetic difference-in-differences (SDiD) estimator. When there is a binary exposure variable where control units are never exposed to the intervention and treatment units have pre- and post-exposure periods, the SDiD parameter can be estimated as follows.
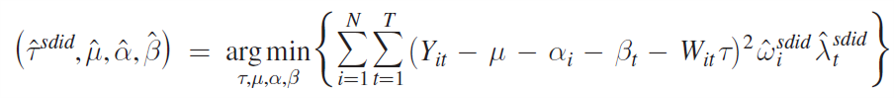
In this equation, the outcome is Yit, the terms μ αi, βt are the intercept, individual fixed effect and time trend respectively. The key parameter of interest is τ which is interacted with an indicator variable for whether individual i at time i is in the treatment group. The approach within the innermost parenthesis is similar to a difference in difference estimation. The key difference is that this difference in difference is weighted by two terms: ωisdid and λtsdid are weights where ωisdid aligns the pre-exposure trends in the outcome of unexposed units with those from the exposed units and λtsdid balance the pre-exposure time periods for the post-exposure time periods. The approach is similar to the SCM estimator however with SCM individual fixed effects, αi, are omitted and there is a single weight, ωiscm, that is used.
The key advantage of this approach is that it allows for a better estimate of the causal effect as the weights make the comparisons more “local” as the approach puts more weight on units that are similar in terms of their past relative to treated units and puts more weights on periods that are similar to the treated periods. This makes the estimates more robust and it also improves the precisions of the estimates. The drawback of this approach is that the estimates are “local” and one should extrapolate the results to the full, unweighted sample with caution. sample
The full article describes in more detail how to estimate the unit weights, time weights and a regularization parameter. Specifically, the unit weights ωisdid are calculated so that the weighted, control group outcomes in the pre-exposure period have a similar trend to the observed unweighted, pre-exposure treatment arm outcomes. The regularization parameter aims to match the size of a typical one- period outcome change for unexposed units in the pre-period, multiplied by a theoretically motivated scaling (NtrTpost)1/4. The regularization parameter is used to increase dispersion when calculating the unit weights. To estimate the time weights, one limits the sample to the control arm observations and weights the time periods in the pre-treatment, control arm outcomes so they look similar to the post-treatment, control arm outcomes.