Let’s say you are interested in measuring the relationship between type 2 diabetes mellitus (T2DM) and depression. In many cases, one would use electronic health records data and conduct a logistic regression with depression as the dependent variable and T2DM (potentially along with demographics and other comorbidities) as the independent variables. However, the use of EHR is potentially problematic. As noted in Goldstein et al. (2016), there is a risked of “informed presence” as the sample of patients in EHR likely differs from those in the general public since individuals only appear when they have a medical encounter.
Specifically, Goldstein and co-authors note that more frequent visits increase the chance of being diagnosed with a disease:
Quan et al. assessed sensitivities based on International Classification of Diseases, Ninth Revision, codes across 32 common conditions. They found that sensitivities for prevalence of a condition ranged from 9.3% (weight loss) to 83.1% (metastatic cancer). Diabetes with complications, for example, has a sensitivity of 63.6%. Therefore, the more medical encounters someone has, the more likely that the presence of diabetes will be detected.
At the same time, while more encounters reduce the likelihood of a false negative, they also increase the risk of a false positive due to rule-out diagnoses.
Since phenotype algorithms are generally designed to detect the prevalence of a condition via ever/never algorithms (you either have the condition or you don’t), the more health-care encounters someone has the higher the probability of a false-positive diagnosis.
Two types of bias may arise:
- Bias to number of physician visits. Figure 1A from this paper shows that the number of encounters may be a confounding factor. It is not evidence, however, whether there is potential for M bias, bias from conditioning on a collider. A collider is a variable that is an outcome of 2 other variables.
- Bias due to general illness. The authors note that a general illness may be the cause of both diabetes and depression. For instance, perhaps someone sustained an injury which lead them to exercise less and eat less healthy (causing T2DM) and the injury itself also increased depression. While my example gives a specific injury, the “general illness” in the Goldstein paper may or may not be fully captured or known. Thus, the authors claim that the number of encounters may be able to serve as a proxy for general illness.
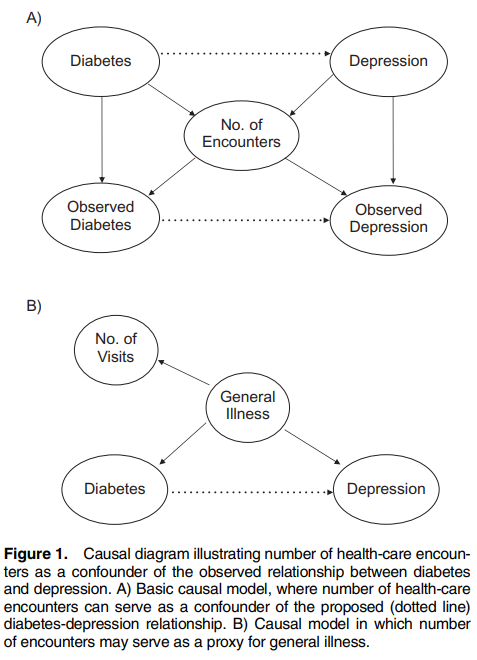
In short, the authors argue that controlling for number of visits can be useful for (i) controlling for the fact that diagnosis is correlated with number of encounters and (ii) number of encounters may be a proxy for general illness.
The authors then conduct a simulation exercise using EHR data from the Duke University Health System. The authors conduct 4 analyses examining the relationship between outcome and exposure controlling for: (i) demographics only, (ii) medical encounters, (iii) Charlson Comorbidity Index (CCI), and (iv) medical encounters and CCI.
The authors summarize their findings as follows:
If the presence of a medical condition is not captured with high probability (i.e., high sensitivity), there is the potential for inflation of the effect estimate for association with another such condition. This potential for bias is exacerbated when the medical condition also leads to more patient encounters…Theory suggests, and our simulations confirm, that conditioning on the number of health-care encounters can remove this bias. The impact of conditioning is greatest for diagnoses captured with low sensitivity.
The authors note that while there is some concern of M bias–as the number of encounters is likely a collider–M bias is likely significantly less problematic than confounding bias in most cases. Others studies (Liu et al. 2012) have confirmed that M-bias is often smaller than confounder bias.
An aside: Berkson’s Bias
The problem of sicker patients appearing in EHR data causes a manifestation of Berkson’s bias:
Because samples are taken from a hospital in-patient population, rather than from the general public, this can result in a spurious negative association between the disease and the risk factor. For example, if the risk factor is diabetes and the disease is cholecystitis, a hospital patient without diabetes is more likely to have cholecystitis than a member of the general population, since the patient must have had some non-diabetes (possibly cholecystitis-causing) reason to enter the hospital in the first place. That result will be obtained regardless of whether there is any association between diabetes and cholecystitis in the general population.