A few months ago, I wrote about what marginal structural models (MSM) were and why one should consider using them in cases where the treatment of interest or confounders vary over time. I linked to how to implement this with statistical programming languages as well.
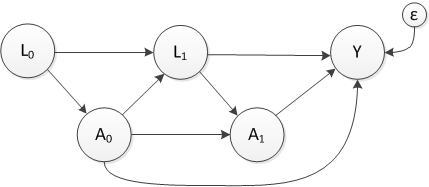
The original paper that developed MSM actually has a very nice example explaining why the inverse probability of treatment weighting (IPTW) is important. The general example is the use of AZT treatment and how the selection of AZT treatment may be influenced based on CD4 counts. The example shows:
- Why to use MSM: If you simple compare outcomes with and without treatment, you will get biased results
- Why weighting works: If you compare outcomes with and without treatment conditional on the confounders and weight these stratified results by the likelihood of the presence of the confounder in the population, you will get the same results.
- Implementing MSM with IPTW. Equivalently, you can use IPTW to create a psuedo-population with weights that are 1 divided by the probability of treatment conditional on the confounder. This new pseudopopulation, unlike the actual population, treatment selection will be unconfounded by confounders as the IPTW is conditional on the confounders. Further, the weighting is such that the causal effect of a given treatment will be the same as the population from the actual study.
- Creating confidence intervals. Although not shown in my example, one can estimate the variance in the parameter of interest using a “robust” or “sandwich” estimator.
- When MSM can fail. MSM can fail in a number of cases. First, there may be unobserved confounders. If these unobserved confounders have a small impact on outcomes and treatment selection, then MSM will still be approximately valid and slightly biased. If these unbiased confounders have a larger impact, then MSM will fail. Second, MSM will fail when an observed confounder perfectly predicts treatment. In this case, the IPTW will be 0 for some of the observations and the weight applied in MSM (i.e., the reciprocal of IPTW) will be infinite. Thus, MSM cannot be calculated in this case.
For more details of how to implement MSM with a simple example from the Appendix of Robbins et al. (2000), please see this file HERE.
Source:
- Robins, James M., Miguel Angel Hernan, and Babette Brumback. “Marginal structural models and causal inference in epidemiology.” (2000): 550-560.