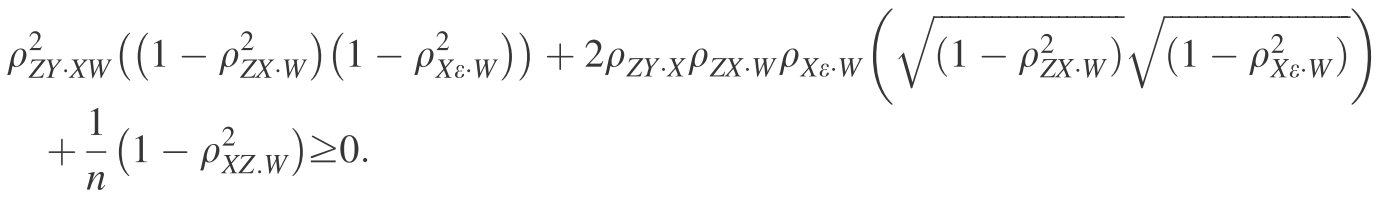When conducting a regression-based analysis, how can you determine whether an instrumental variables (IV) method is better than an ordinary least squares (OLS) method? A paper by Basu and Chan (2013) describes one approach based on measuring which of the approaches most successfully reduces the mean square error (MSE) of the coefficient of interest. IV has a lower MSE than OLS when:
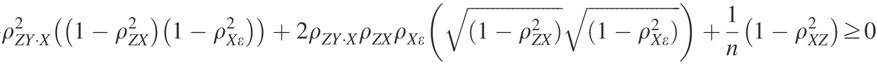
The term ρZX indicates the correlation between instrument (Z) and the variable of interest (X). The term ρZY,X is the partial correlation between the instrument (Z) and the outcome of interest (Y) conditional on the variable of interest (X). One can calculate the partial correlation in two steps. First calculate residuals for Z and Y by separately regressing each on the conditioning variable (X). Next, calculate the correlation between the regression variables.
Note that one can calculate all terms above from the data except the correlation between X and the true residual ε (i.e., ρXε). Nevertheless, if one has a reasonable estimate for this correlation—in essence, a reasonable bound for the bias that OLS would introduce—then one can use this tool to determine whether the IV approach can produce a better estimate the OLS (in MSE terms).
In most situations, the primary regression interest includes not only the variable of interest but also other covariates (W). In this case, one can modify the equation above by calculating partial coefficients. Note that ρZY,XW is the partial correlation between Z and Y after controlling for X and W.
The paper also discusses how to apply this approach in the presence of multiple instruments.
Source:
- Basu, A. and Chan, K. C. G. (2013), CAN WE MAKE SMART CHOICES BETWEEN OLS AND CONTAMINATED IV METHODS?. Health Econ.. doi: 10.1002/hec.2926